
Disponible en
Español
![]()
CEMLA Course: Financial Mathematics
November 11 - 15, 2024
Videoconference
CEMLA organized the CEMLA Course: Financial Mathematics, which was held virtually from November 11 to 15, 2024. The course featured the participation of 106 representatives from 25 member institutions, associates, and collaborators of CEMLA, spanning 22 countries. During the event, key stochastic and numerical models used in derivatives and bond markets were presented.
In the first session, anecdotes about the use of financial instruments were shared, along with a brief overview of the development of financial mathematics. Stochastic calculus was introduced to model market uncertainty, starting with random walks, transitioning to Brownian motion as a continuous limit, and culminating in stochastic differential equations and Itô’s lemma.
The second session focused on the Feynman-Kac theorem, which connects stochastic differential equations with the Cauchy problem in partial differential equations, leading to the derivation of the Black-Scholes formula. The session concluded with practical applications for pricing vanilla options in real markets, comparing theoretical results with observed values.
In the third session, the Put-Call parity relationship and other parity relationships were explained. Additionally, position hedging using replicating portfolios was analyzed, employing the Black-Scholes formula for approximations.
The fourth session concentrated on the binomial model to determine periodic rebalancing of hedging portfolios. Monte Carlo simulations for option pricing were also explored. The day ended with the introduction of investment strategies focused on trends and volatility.
Finally, the fifth session formalized the use of these strategies. The course concluded with an introduction to fixed income theory, modeling zero-coupon bonds from three perspectives: short-term interest rates, forward rates, and direct bond pricing. Notable models such as Vasicek, Cox-Ingersoll-Ross, Dothan, and Hull-White were highlighted.

III CEMLA-Dallas Fed-IBEFA Workshop on Financial
Stability
Frontier Research in Financial Intermediation
Call for Papers
November 25 – 26, 2024 – Mexico City, Mexico
The Center for Latin American Monetary Studies (CEMLA), the Federal Reserve Bank of Dallas, and the International Banking, Economics and Finance Association (IBEFA) invite submissions to their 3rd Financial Stability Workshop, to be held on November 25 and 26 2024 at CEMLA’s offices in Mexico City. We invite theoretical and empirical submissions focusing on the interplay between financial intermediation, banking, and financial stability, on topics including:
- Interactions between monetary policy, inflation dynamics, and financial stability
- Lending technologies and FinTech
- Financial fragility through cross-border spillovers
- Liquidity risks and wholesale funding markets
- Climate finance
- Risks in housing and real estate markets
- Latest developments in prudential policies and regulation
CEMLA invites submissions for a special sponsored session dedicated to discuss outstanding research relevant for Latin America and the Caribbean.Authors indicating in their submission a preference for a dual-track submission will have publication opportunities in the Latin American Journal of Central Banking.
Participants are expected to cover their travel expenses; sponsors will offer to cover accommodation for invited participants. Please submit papers to: fsworkshop@cemla.org using the subject line “Submission – FSW”. Submission deadline is May 27, 2024. The authors will be informed of the final acceptance in early July 2024.
Keynote Speaker
- Viral V. Acharya, New York University Stern School of Business
Scientific Committee
- Christoph Bertsch, Sveriges Riksbank
- Mauricio Calani, Banco Central de Chile
- Ricardo Correa, Federal Reserve Board
- Matteo Crosignani, New York Fed
- Mariela dal Borgo, Banco de México
- Scott Davis, Dallas Fed
- Filippo De Marco, Bocconi
- Ralph de Haas, EBRD
- John Duca, Oberlin College
- Paul Fontanier, Yale School of Management
- Emilia Garcia-Appendini, Norges Bank
- Gabriel Jiménez, Banco de España
- Peter Karlström, CEMLA
- Thomas Lambert, RSM Erasmus University
- Elena Loutskina, Darden School of Business Administration
- David Martinez-Miera, Universidad Carlos III de Madrid
- Natalya Martynova, Deutsche Bundesbank
- Sergio Mayordomo, Banco de España
- Karsten Müller, NUS Singapore
- Carola Müller, BIS
- William Mullins, UC San Diego
- Pascal Paul, San Francisco Fed
- Andrea Presbitero, IMF
- Claudio Raddatz, Universidad de Chile
- Raluca Roman, Philadelphia Fed
- Kasper Roszbach, Norges Bank
- Farzad Saidi, University of Bonn
- Alessio Saretto, Dallas Fed
- Larissa Schäfer, Frankfurt School
- Glenn Schepens, ECB
- Jason Sturgess, Queen Mary University
- Rimmy E. Tommy, The University of Chicago Booth School of Business
- Lena Tonzer, Magdeburg University, IWH
- Nitzan Tzur-Ilan, Dallas Fed
- Alexander Ufier, FDIC
- Bernardus van Doornik, Banco Central do Brasil
Program Co-chairs
- Matias Ossandon Busch, CEMLA
- Enrique Martínez García, Dallas Fed
- Lars Norden, FGV, IBEFA
- Björn Imbierowicz, Deutsche Bundesbank, IBEFA

III CEMLA-Dallas Fed-IBEFA Workshop on Financial
Stability
Frontier Research in Financial Intermediation
Call for Papers
November 25 – 26, 2024 – Mexico City, Mexico

III CEMLA-Dallas Fed-IBEFA Workshop on Financial
Stability
Frontier Research in Financial Intermediation
Call for Papers
November 25 – 26, 2024 – Mexico City, Mexico
Viral V. Acharya
Viral V. Acharya, C.V. Starr Professor of Economics at NYU Stern, is a leading figure in financial economics. Former Deputy Governor of the Reserve Bank of India, his research focuses on systemic financial risk and its regulation, including climate-related risks. He has received prestigious awards and is a highly cited researcher. Currently, he serves on editorial boards, including the Journal of Law, Finance and Accounting, and is a member of the Climate-related Financial Risk Advisory Committee (CFRAC) of the Financial Stability Oversight Council for 2023-26. He is also Research Associate of the National Bureau of Economic Research (NBER), Research Affiliate at the Center for Economic Policy Research (CEPR), and Research Associate of the European Corporate Governance Institute (ECGI). With a background in computer science and engineering, he earned his Ph.D. in Finance from NYU-Stern.

III CEMLA-Dallas Fed-IBEFA Workshop on Financial
Stability
Frontier Research in Financial Intermediation
Call for Papers
November 25 - 26, 2024 – Mexico City
Venue Information
CEMLA is located in Durango 54, Col. Roma Cuauhtémoc, C.P. 06700 Ciudad de México, México; near downtown Mexico City.
Mexico City is located near the center of the country, at an average altitude of 2,300 meters above sea level, bordering the State of Mexico and the state of Morelos. The capital is connected by land to multiple destinations.
Time Zone
Mexico has a time difference with Greenwich Mean Time of -6 hours.
Weather
In Mexico City, the wet season is warm and overcast and the dry season is comfortable and partly cloudy. Throughout the year, the temperature usually ranges from 6°C to 26°C and is rarely below 3°C or above 30°C.
The warm season lasts for 2.5 months, from March 22 to June 8, with an average daily temperature above 20°C. The hottest month of the year in Mexico City is May, with an average high of 27°C and low of 13°C.
The cool season lasts for 2.5 months, from November 19 to February 3, with an average daily high temperature below 22°C. The coldest month of the year in Mexico City is January, with an average low of 6°C and high of 22°C.
Visa Information
All participants are responsible for all Passport and visa formalities, and if needed, to comply with health regulations.
Citizens of certain countries require a visa to enter Mexico. In the following link you will find a list of citizenships which require visas: Countries that require visas.
Exceptions apply if you have a visa or if you are a permanent resident of the United States, Canada or Europe. If you are a citizen of a country requiring a visa, please contact the closest Mexican consulate at: Mexican consulates. For more information, please click here.
If you require an invitation letter in order to obtain the visa, please email Eréndira Fuentes Hernández (fuentes@cemla.org) specifying your current affiliation and title of the paper that you will be presenting.
Currency and Exchange Rate
Official currency: Mexican peso (MXN).
For the updated exchange rate click here.
You will be able to make currency exchanges at exchange houses and in some bank offices. It is recommended to exchange money at the airport since exchange houses and banks near CEMLA and the suggested hotels are closed on weekends, and close early during the week (around 16:00 hrs). Usually, ATMs are available 24 hours. You may draw cash using international debit and credit cards with worldwide brands, like Visa, Mastercard, Visa Electron and Dinners. For more information, please visit Banco de México.
VAT and others
- · VAT: 16%.
- · Hotel service: additional charge of 3.5% on top of lodging (ISH or lodging tax).
- · Tips at restaurants: from 10% to 15% depends on the service you have received.
Electricity Service
Energy: 127 volts AC at 60 cycles (127V AC, 60 Hz). Two flat-pin plugs and some with grounding.
Transportation
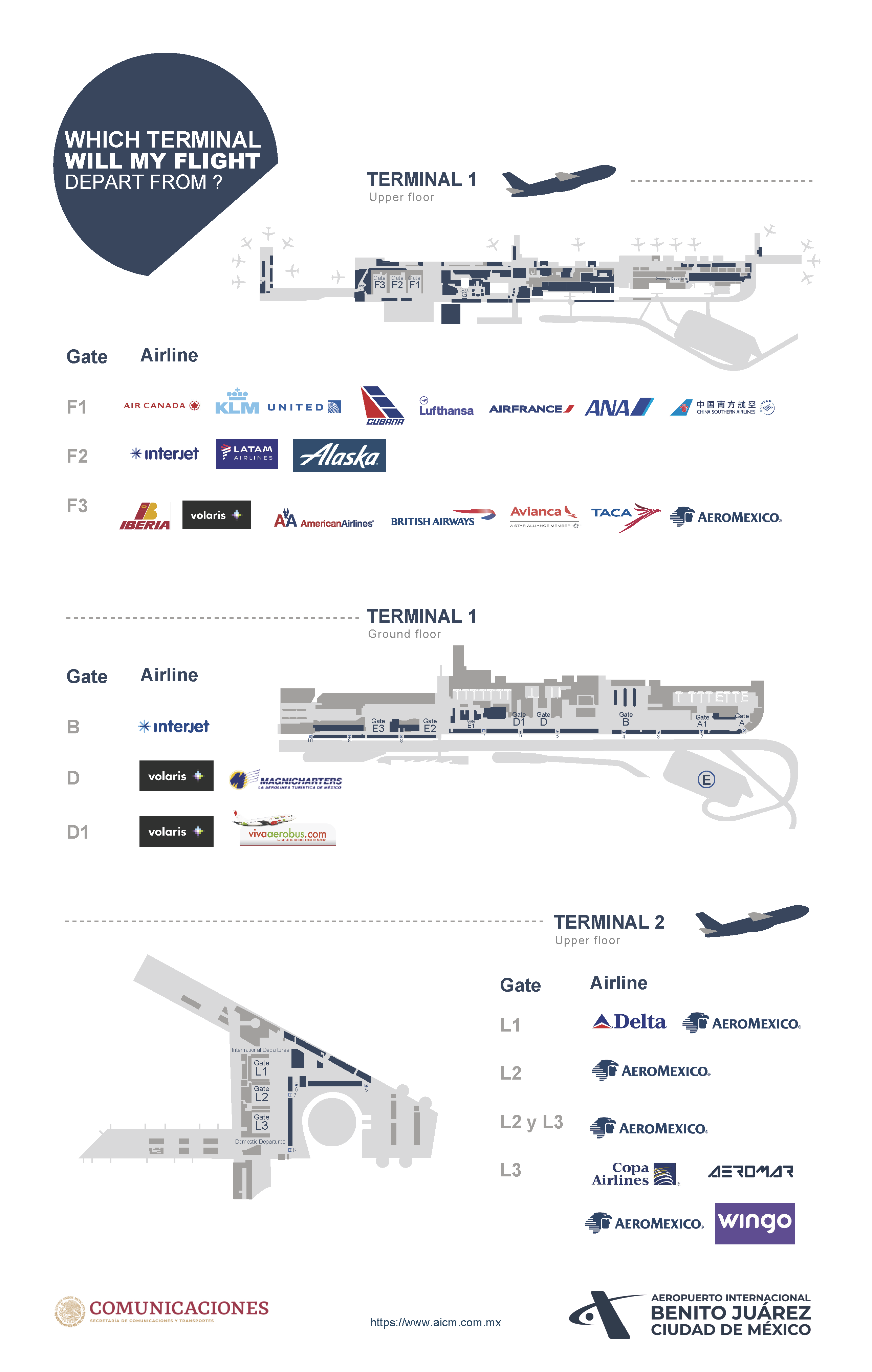
The Benito Juárez International Airport in Mexico City is located 13 kilometers from the Downtown. It has two terminals which are identified by Terminal 1 and Terminal 2 and both are connected by aerotrain and free bus transportation. For more information, you may find the airport website here.
When arriving to Mexico City, transportation from the airport to hotels can be done by transportation apps (such as Uber, Cabify, Didi and Lyft, among others), or taxi. For taxi transportation it is important to select a taxi company inside the airport (there are different options to select from once you exit customs and immigration), pay the cashier inside the airport and ask for the cab in the corresponding exit. The Mexico City International Airport (AICM) offers spaces or boarding areas for the use of authorized cabs accredited by the Ministry of Communications and Transportation (SCT) and regulated by the Airport, for more information on authorized cabs click here.
For transportation in Mexico City, we recommend participants to use transportation apps or taxi service taken from “SITIO” stands. We recommend that participants avoid taking taxis from the street. SITIO stands can be found in several locations and phone numbers to call for taxis can be obtained in the hotels.
CEMLA will not provide transportation services.
Accommodation
The following table shows CEMLA’s recommended hotels, the rates available to events participants and hotel contact information. Booking hotel is the visitors’ responsibility. Consider that hotels usually request a credit card to guarantee the reservation. Consider that hotels usually request a credit card to guarantee the reservation. Rates include 16% VAT and 3.5% ISH (local tax).
To receive the corporate rate in the recommended hotels you must specify the name of CEMLA. Any change of rates is the responsibility of each hotel. Even though some bookings can be made online we recommend contacting the hotel directly to make sure the group rate is given.
Recommended Hotels
Hotel
Rates
Reservation information

Stanza
Av. Álvaro Obregón 13, Roma Nte., Cuauhtémoc, 06700 Ciudad de México, CDMX
(3-minute car trip, 6-minute walk, 500m to CEMLA)
Ordinary rate per night:
$ 125 USD
CEMLA corporate rate:
$ 83 USD, includes taxes
Phone: + 52 55 5080 0900

Royal Reforma
C. Amberes 78, Juárez, Cuauhtémoc, 06600 Ciudad de México, CDMX
(10-minute car trip, 13-minute walk, 1 km to CEMLA)
Ordinary rate per night:
$ 165 USD
CEMLA corporate rate:
$ 81 USD
Includes:
Taxes, Wi-Fi, breakfast buffet, gym, pool, sauna (upon request)
Phone: +52 55 9149 3000

Four Points by Sheraton
Av. Álvaro Obregón 38, C. U. Benito Juárez, Cuauhtémoc, 06700 Ciudad de México, CDMX
(5-minute car trip, 6-minute walk, 500 m to CEMLA)
Ordinary rate per night:
$ 210 USD
CEMLA corporate rate:
$
114
USD
accommodation
only
$
130
USD
accommodation
and
buffet
breakfast
Includes:
Taxes, Wi-Fi, fitness center
Phone: +52 55 1085 9500

City Express Plus Reforma El Angel
Av. Paseo de la Reforma 334, Juárez, Cuauhtémoc, 06600 Ciudad de México, CDMX
(10-minute car trip, 20-minute, 1.6 km walk to CEMLA)
Ordinary rate per night:
Please consult directly with the hotel.
Includes:
wi-fi, breakfast
Phone: +52 55 5228 7800

Sheraton Mexico City María Isabel
Av. Paseo de la Reforma 325, Cuauhtémoc, 06500 Ciudad de México, CDMX
(13-minute car trip, 21-minute walk, 1.6 km to CEMLA)
Ordinary rate per night:
According to demand
CEMLA corporate rate:
$ 198 USD
Includes:
Taxes, Wi-Fi, breakfast buffet, gym
Phone: +52 55 52425672

Marriot Reforma
Av. Paseo de la Reforma 276, Juárez, Cuauhtémoc, 06600 Ciudad de México, CDMX
(15-minute car trip, 17-minute walk, 1.3 km to CEMLA)
Ordinary rate per night:
$ 419 USD
CEMLA corporate rate:
$ 207 USD
Includes:
Taxes, Wi-Fi in business center, breakfast buffet, gym
Phone: +52 55 1102 7030

Brick Hotel
Orizaba 95, Roma Nte., Cuauhtémoc, 06700 Ciudad de México, CDMX
(6-minute car trip, 7-minute walk, 500 m to CEMLA)
Ordinary rate per night:
Please consult directly with the hotel.
Phone: +52 55 9155 7610
Map
Visit Mexico
Mexico City is a unique visitor destination offering a wide range of attractions combining historic and modern-day life in a vibrant and friendly atmosphere. Take a day to visit the pre-Hispanic ruins of Teotihuacan, or visit the Centro Histórico and marvel at its rich architecture form the Catedral and Plaza del Zócalo to Palacio de Bellas Artes, visit world-class museums, or spend the day at some of the modern-day bustling neighborhoods and enjoy a fine dining experience at some of the world’s top-rated restaurants. For more information visit: Official Mexico City Visitors' Guide | Guía oficial para turistas de la CDMX Mexico City.
Dinning
Mexico City offers a wide variety of restaurants most of them located in the tourist areas of Polanco, Roma and Condesa near the Conference Venue.
Sightseeing/Day trips
If you are planning to stay an extra day or two in Mexico City, we recommend taking a day to visit the Centro Histórico, Coyoacán, Reforma Avenue, Colonia Roma, Xochimilco, and Chapultepec.
A day trip to Teotihuacan to see the pyramids can be arranged with the hotel concierge.
Mexico City offers some world class museums including the Anthropology Museum, the Museo Soumaya, and the Interactive Museum of Economics.
COVID-19 Protocol
CEMLA Health Protocol based on the suggestions of the Pan-American Health Organization
- Body-temperature checks and provision of hand-sanitizing gel and face-masks at the entrance of our facilities.
- Limited capacity in rooms to comply with a minimum distancing of 1.5m between individuals.
- Rodrigo Gómez Auditorium has been equipped with an air-ventilation system with UV-C light air purifiers and air-exhaust systems.
- Javier Marquez Room, Multimedia Room, restrooms and boardrooms, among other rooms, have been equipped with UV-C light conditioning.
- CO2 and humidity monitors in the main spaces of the building.
- Open-door room policy.
- Cleaning and maintenance plans after regular occupation hours.
- Regular updates based on the tracking of recommendations of the health authorities in Mexico and International Organizations.

III CEMLA-Dallas Fed-IBEFA Workshop on Financial
Stability
Frontier Research in Financial Intermediation
Call for Papers
November 25 – 26, 2024 – Mexico City, Mexico





